Plant Genomics & Developmental Biology Consultant / Expert Offering Creative Paradigms for Scientific Advancement in Agriculture and Medicine, with Emphasis on Plant Genetics / Genetic Engineering and Developmental Biology, e.g., Organogenesis. Michael M. Lieber, Ph.D. Berkeley, CA (510) 526-4224

 Biography

 The Golden Ratio as a Dimensionless Biological Constant Enabling a Dynamic Uniformity in Specificity and Diversity within Various Self-Similar Scales in Natural Phenomena: Its Operation within the Universal, Dimensional Physical Constants and Enabling  Fractal Realities

                                        Part I:  The Dimensionless Biological Constant and Forces 

 In an earlier publication (Lieber, 1998a), this author demonstrated that many, if not all, of the universal, dimensional physical constants of physics have either as an underlying common component a dimensionless constant equal to the golden ratio (1.618) or its reciprocal, or in some cases combinations of both or powers of both. Such a constant was referred to as a biological dimensionless constant, as it was shown to represent biological properties or features, such as regenerative, vortical growth in plant development. As noted, the golden ratio represents a constant, universal rate of such vortical or spiral growth. This would be a universal rate or situation, and thus, it was  proposed, to be applicable to the universal dimensional constants of physics. To this end, specifically, this was also shown to be a dimensionless situation or factor within the universal, dimensional physical constants, independent of the system of units.

 Such a  situation was allowed to be detected through a constant parameter, π. It is π through which the metric system is based, and which the physical dimensional constants use. (See, Lieber. 1998a. View the PDF of Article.) Specifically, the biological dimensionless or trans-dimensional constant, referred to as Q in this article, rather than as Φ, reflects or defines an inherent, constant proportion of vortically regenerative growth as a universal, guiding, patterning template-feature or design within and necessary for the emergence and maintenance of all natural phenomena, biological as well as physical. That is, this would be a constant, vortically regenerative, significant and guiding template-feature, through which, the non-uniform physical forces would arise. And through such non-uniformity, force uniformity would necessarily occur by dynamic completion via that very dynamic  of vorticity. These very forces of non-uniformity and completing uniformity would arise, and manifest geometrically, through  that vortically guiding regeneration. This would occur first through a plenum or manifold underlying a space-time field, and then, emerging into and via the space-time field. Such vortical regeneration, continuing via space-time through an implicit process, would become geometrically manifest at times as self-similar, logarithmic spirals within and necessary for developing phenomena. This would be especially the situation within many developing living organisms.

This implicit vortical regeneration would reflect a universal drive towards dynamic completion within all emerging phenomena and their sustainability. And this would include all completing forces involved in the maintenance and progressive stabilization of such phenomena through force-based geometries or configurations. Specifically, this is the drive to generate a uniformity of forces within emerging and sustained phenomena made up of non-uniform forces. And this drive would be manifested as a drive towards dynamical completion within  those phenomena, which further manifests as growing dynamical stability of such phenomena. This would also be manifested through the dynamical geometries of those phenomena. In other words, such progressive stabilization of phenomena would occur through  resolving, via vorticity, those very non-uniform constraints or forces into uniformity through the shaping of the force-determined geometries of those phenomena. Such non-uniformity would arise through that  very vorticity. and utilized by vorticty to generate uniformity within the non-uniformity of forces. Through vorticity, these non-uniform and uniforming forces would be generated firstly via a plenum and then via the space-time field. This generating uniformity of forces within the non-uniformities, which defines specificity in nature, would continually occur through an inherent constant vorticity. And such vorticity would be, underlyingly, in the emerging and sustained phenomena. This would enable the emergence of dynamically stable geometries of those phenomena. These phenomena, with their progressively stable geometries of force, would hence emerge via the plenum and space-time through an imprinting vorticity, which creates vortical currents of plenum.

 Through such vortical currents, completing and guiding forces would arise. And these forces would ensue in structurally guiding geometries of completing force in sustaining phenomena. This would involve or enable the  structurally stabilizing  geometries to occur via  completing forces within such phenomena. And these phenomena  would be consequently and continually generated  through  space-time at various scales. This generative process within developing phenomena would occur via a constant rate of self-similar, regenerative voracity through currents in a plenum. Such dynamical completion would, via vortical currents,  progress in space-time.  And this would  also involve the space-time within each of the emerging and sustained phenomena or phenomenological systems. To reiterate, this would occur  through  an ongoing, guiding and underlying, vortical regeneration  initially via a plenum. The consequence of such would be the progressive stabilization of such phenomena through their dynamical completion within their geometrical structures. And this would occur within space-time. In effect, such  force-involved geometrical structures, many fractal, composing phenomena emerging in space-time, would have themselves occurred through an underlying vortically dynamic geometry. This would be a geometry manifested as self-similar spirality in space-time. Such a guided dynamic process would be especially emphasized in living phenomena. The physicist, Paul Lieber described a variation of such a drive towards dynamical completion in a 1969 publication.

     As the author illustrates as to feasibility, this pattern of force generation and patterning, involving completion, emerges and manifests through those particular geometrically-patterned constraints, or non-uniformities of force, manifested by the dynamical geometries of emerging and sustained phenomena. And these phenomena would only be allowed by or enabled vortically through the regenerational drive manifested by that specific, inherent template within the plenum. This is the guiding, vorticity-inducing template that the dimensionless or trans-dimensional constant, Q (or its reciprocal Q^-1 ) represents or defines or reflects. Also, manifested  through those emerging and sustaining geometries of dynamical phenomena would be that golden-ratio, template of  a  constant rate of  spiral growth. This is the template of growth that  also enables and patterns, through a spiral dynamic,  progressively stable, completing geometries of force within force non-uniformity, as phenomena of space-time. Because of such, a maximum  or increasing uniformity of force can be generated throughout and can utilize completely or uniformly the space-time involved  in those phenomenological geometries. Within and via such  dynamical geometries, the very generation of these completing forces would continue. And these completing forces, and their completing patterns within and via spatial-temporal phenomena, would be guided and enabled concurrently by and through the underlying currents of vorticity.

 By virtue of dynamic non-uniformities or constraints within such geometries manifested by phenomena, the drive  towards dynamic completion would occur, drawing on completing forces occurring through spiral currents. In effect, the completion dynamic or drive occurs in non-uniform phenomena, which themselves have emerged ultimately through a constant, vortical regeneration drive and guidance. Yet, these geometrical constraints or non-uniform forces within phenomena would allow or enable the  very dynamical completion within such phenomena.  And this drive for dynamical completion within phenomena, or their geometrical-dynamical designs, would also be enabled or supported by a concurrent, underlying drive for  a guiding, vortical regeneration via spiral currents.  Hence, these would be phenomenological designs, many of which could themselves be stably vortical in design, that themselves are allowed or ultimately enabled  through the Q template, its drive, to occur via the Q spiral of generation.  In effect, within phenomena, their geometrical constraints, or non-uniformities of manifested force,  there is a drive for the completion of force configurations, a drive for  a uniformity within the non-uniformity of such force configurations, which are expressed through the progessive emergence of stable geometries of force. And that drive would be enabled by or occur through the drive for vortical regeneration within and via a plenum.

 Such resolution of geometrical constraints or non-uniformities of force, towards  dynamical completion, within and between joined phenomena, occurring in and connected to space-time, may also call upon an inherent impenetrability in the plenum and the space-time field. Impenetrability enables forces or constraints and thereby the vortical currents within the plenum and space-time. Q reflects a constant proportion of vortical, self-similar growth (involving constraints) within and  manifested by respectively growing, self-similar logarithmic spirals. It is through the generative design and guidance of self-similar spirals that the phenomenological, completing features of existence arise via a plenum and space-time. And  these are sustained through a guided, dynamical, and stable completion via space-time that could be marked by, or occur through, such spiral growth and its associated forces of completion.

 This would be especially the vortically self-similar dynamic avenue whereby fractal features or structures can also emerge into existence. And many of these features would themselves manifest or display self-similar, vortical characteristics supported by completing forces, arising through that very vorticity via a plenum and space-time. Such dynamic, phenomenological characteristics would be stable or relatively complete through a uniformity of force within such, their force-supported geometries. In effect, by means of vortical guidance, enabled through an inner template reflected through Q, geometries (many fractals) would emerge, and, from and through such geometries, stabilizing, curvilinear forces, as uniformities of force across all scales, would become manifest. And these would be revealed to us as dynamic fractal phenomena, also geometrically manifested in living organisms. Our physics, its limited methodology, would reveal these force-patterning geometries, and reciprocal force manifesting geometries, in a different manner.  Such a methodology would describe these guided dynamics as  the merging of mass, energy, and force with, within and from the various curving milieus of space-time. As Albert Einstein once stated, "A thrown stone is but a change in the [space-time] field." (See, Einstein and Infeld,1938.) Yet, his creative approach did not allow for the detection of a deeper principle pertaining to the universe's dynamics.

    As pointed out first by G. B. Riemann in 1854 and then by W. Clifford (circa, 1899), forces could be determined by or arise through curvatures within space, that is through geometry. Subsequently, A. Einstein, using Riemann's mathematics, creatively and elegantly demonstrated in various publications that gravitational forces and their patterns are due to or are marked by, or manifested through, curvatures within a space-time metric field, which are influenced or structured by means of matter-energy and its inherent geometry or architecture. And this could be a geometry or architecture having Q as a constant and enabling/shaping parameter involving the impenetrability of the very intense mass-energy field. In fact, it can be shown through the author's analysis that  Q^-1 is a component of the field equations that Einstein used to describe gravity and matter, suggesting that such fields in relation to mass (and mass reciprocally to such fields) have a constant and regenerative parameter. (See Table 1.) In effect, mass-energy and its geometry would give rise to the space-time curvatures, which would guide and manifest the gravitational forces regeneratively in space-time, while these very curving forces would also regeneratively determine or manifest the space-time geometries of curvature. This iterative, retroactive, reciprocal dynamic process, involving geometry and force, could itself have a helical or vortical pattern in space-time.

    Though not addressing this particular possibility regarding a universal constant's relevance to matter-energy's generation of curvatures in space-time, Dr. Einstein's theories have nevertheless been supported experimentally. Dr. Clifford further pointed out that magnetic forces could be due to or manifest twists within space, that is, geometrical twists of space.  If this were the situation, might these twists within space, or within a space-time metric field, be spirals whose parameters are defined and enabled by what Q reflects via space-time? Many developments in physics have attempted to unite the various forces of nature, such as gravity and electromagnetic forces, as unified distortions of a space-time metric at higher dimensions. Q could extend to and be involved in such dimensions by virtue of what Q reflects, and thereby the specific and unifying  forces allowed by or expressed through such dimensions.

     In view of the significant role of generative processes reflected by the dimensionless components of the physical dimensional constants, let us first take a look at a physical dimensional constant and see how the regenerative component, sub-constant Q or its reciprocal Q^-1, may play a role, and thereby in the operation or maintenance of an important physical constant. In light propagation, the speed of propagation of the electromagnetic wave or field is 3 x 10⁸ meters per second or 5(Q^-1) x 10⁸ meters per second. This speed in a vacuum is a universal constant, denoted by c. Due to Q or due to what it represents or means, such a propagation would indicate a represented regeneration enabled by what Q^-1 (or Q) allows geometrically within the dimensional constant. This would also suggest a wave propagation of electromagnetic forces of maximally uniform symmetry within the entire region of spatial propagation. In situations where light would manifest photon/corpuscular characteristics within the propagation as compact, coherently connected wave-packets, such propagation would be of the maximum uniformity of the forces between the photons and a maximum uniformity within the geometrical relationships between the specific photons themselves.

    The geometry of propagation might also indicate the operation of a constant endemic universally to various geometries, and that constant is pi or Π ( π ). And in fact, this constant is readily evident in the expression of the speed of light constant, namely 5Q^-1 x (π² )⁸ meter per second, where 10 equals π². In fact, wherever 10 is present in the dimensional constants, which is in every one of such, π² can be substituted. This again indicates an inherent, non-dimensional constancy, underlining the dimensional constants, yet geometrically defining with regard to uniform force patterns maximally displayed within space and time.

    A important connection between π and Q is thus indicated regarding the maintenance of the underlining dimensionless constancy within the dimensional constants due to the regeneration involving forces and their uniformity of manifestation. This connection is also seen in some mathematical equations: In various, complex trigonometric equations or expressions Q can be expressed in terms of π, where in other trigonometric equations, π is expressed in terms of Q. (See Posamentier, A. & Lehmann, 2012.) These expressions might also point to constant relationships within physical phenomena, perhaps involving self-similar waves, yet to be discovered. Trigonometric functions do in fact describe electromagnetic phenomena, such as waves, and the Fourier series shows how trigonometric functions combine into complex wave-functions, which describe actual physical wave behavior in fluid dynamics.

    In a well known physical-chemical situation, there is the operation of Avogadro's constant. This is a remarkable transcalar and trans-chemical constant, which points to quantifiable identities or uniformities of number of different physical entities, from  atoms to molecules, within the scale of the gram-weights of all chemicals. This, thereby, links uniformly in terms of a constant number all of these different physical entities, across different levels of their structure, through various chemicals in a self-similar manner. Furthermore, within the scale of the gram-mole of any molecular compound, the number of molecules would be the same at the number of atoms within the scale of a gram-atom, irrespective of the structural size of these different chemical entities and irrespective of the particular chemical making up of such entities. This is constancy of number within variation and independent of scale of mass.  Furthermore, this would be a transcalar constant that expresses and unites the constancy of various mass-weight proportions of various chemicals through and within different scales, from atomic weights to molecular weights, through to various gram weights. Such constancy also expresses and unites through different chemical elements and molecules.

   The constancy of such various weight-mass proportions of different chemicals depends on and is manifested through the same constant number of atoms and molecules of various chemical elements and molecules at a given weight or mass scale, which is independent of the particular element or molecule. The effective application of the gram-atom and the gram-mole within chemistry has been based upon this constant number of atoms and molecules, enabling constant numerical values of chemical proportions of weight within and across different scales of mass-weight. Across the different weight scales, the  numerical values of these weight-mass proportions remain the same, that is, constant.

   To go from the atomic weight scale, or from the molecular weight scale, to the gram weight scale or gram-atom or gram-mole scales, one multiples by the constant  number of atoms or molecules represented by this constant to achieve the same  numerical value of weight of an element or molecule at the gram level as its  numerical value is at the atomic or molecular level. This number or scalar remains constant irrespective of chemical element and molecule. The gram-atom is thus: that quantity of the chemical element, such as sulfur, whose weight in grams is numerically equal to its atomic weight. And the gram-mole is that quantity of a molecule, such as water, whose weight in grams is numerically equal to its molecular weight.  And it takes respectively the same constant number of atoms and molecules to respectively obtain the gram-atom and the gram-mole. And this constant remains constant irrespective of the type of chemical. It represents constancy within chemical variation as well as between scales of mass or weight. Moreover, this constant  also connects the sub-atomic scale to the gram-weight scale with regard to the number of electrons: The number of electrons composing the gram-atom-weight scale of any element is always equal to the atomic number of that element multiplied by Avogadro's constant. This could be considered as the gram-electron scale.

   This constant number is denoted by Avogadro's constant. This dimensional constant in terms of Q and Π (π ) is Π² Q^-1 x (π²)²³ molecules per gram-mole or atoms per gram-atom of any chemical. Significantly, this constancy of number of entities at the gram level of mass, whether of atoms or molecules, and independent of their chemical variation or types, has become evident through the constant maintenance of higher scale quantities, that of the gram-atom and gram-mole. And the constant relationship between the gram-electron scale, the gram-atom scale and the atomic weight scale, and between the gram-mole scale and the molecular weight scale, is the Avogadro's constant, which is a constant that also unites different atoms and molecules, but is independent of their variations. Moreover, this constant demonstrates a constant scalar relationship between the  the gram-electron,  the gram-atom and the gram-mole. The  gram-electron, the gram-atom and the gram-mole define and unite constantly via Avogadro's constant respectively physical entities of different masses, structures, and scales. Significantly, the determination of this constant number involved a calculation using the constant of the electric charge, Q x (π²)^-19 coulombs. Q may very well facilitate the constant, transcalar operation or direction, pertaining to mass scale, mass type and mass structure, of the Avogadro constant. More inclusively, a universal correspondence of different structures or morphologies is indicated here, dynamically mediated through Avogadro's  constant and Q.

   The foregoing account again shows the operation and significance of dimensionless or trans-dimensional constants  within another dimensional constant, the Avogadro's constant, but nevertheless, linking all dimensional constants together. (See Table 1 listing many of the dimensional constants wherein Q or Q^-1 and π are evident.) As one reviews the various dimensional physical constants, one sees how Q and π become repeatedly revealed. Though the relationships between Q and π (or between the various forms of Q such as Q^-1 and Q² ) may change within the expressions of the different dimensional constants or from constant to constant or from metric unit to metric unit, Q in its various forms will always appear and will appear constantly with π² or at times with π. We see this with the Boltzmann dimensional constant, which defines or applies to a situation where the entropy of energy or its uniformity increases maximally through space and time. This is a situation that could be described as an evolving, physical system towards maximum uniformity, but not uniformity within specificity or diversity. When the physical units of this constant are in terms of calories and degrees centigrade, this constant is written as 2Q x (π² )^-24 cal/^oC. However, when the units of that constant are in terms of joules and degrees Kelvin, the constant becomes expressed as 1+Q^-1/Q x (π²)^-23 joules per degree Kelvin.

     The various relationships of these different forms of Q evident through the various dimensional constants might be constructed into some type of periodic table. Such a table might provide deeper meanings of these relationships and more insight as to how the various constants repeatedly relate more fully and completely to one another through repeating patterns involving Q and Q^-1. Though, the dimensional constants being unified by a force regeneration and force display, defined or patterned by Q and its forms, is also a important revelation. Nevertheless, it is important to emphasize, such a periodic table of the various combinations of the forms of Q through the dimensional constants might further reveal a common physical self-similarity of generation of force patterns across different levels of organization within and between different phenomena. In this regard, as the Planck's constant, the quantum of action, involving force through time, refers to a constant feature of the quantum-energy process on the micro-level of reality. This constant feature marks a stability at the atomic and sub-atomic level of reality. And, as the cosmological level of reality is defined by the gravitational constant.

And, as both of these constants have in common Q, as shown in Table 1, this would suggest that Q  also refers to or defines a self-similar or transcaler process or pattern involving forces, which is common to both realms or levels of physical-geometrical organization. Stable quantum structuring is marked by Q in Planck's constant. Such quantum structuring occurring through intersectional, stabilizing self-similar, vortical regenerations, would manifest as discontinuities of morphologies through mass/energies at micro-scales and into the macro-scales of space-time. As noted, this would be mainly manifested at the macro-level of space-time  through the  stabilizing, morphological developments within living organisms. (Also, see Lieber, 1998a. View PDF of Article.). Thereby, Q  is  seen as also trans-dimensional in structuring, self-similarly, stable discontinuity through self-similar regenerating, intersectional continuities via different scales of space-time. Such structuring of quantum discontinuities would be exhibited through the generation of connected fractals.

     This generation of such stable, connected self-similarity on different scales, guided or allowed geometrically-physically by Q or its forms, could predictably be the generation of increasing degrees of force uniformity within specificity or diversity (non-uniformity) on different scales and between such scales. And such increasing force uniformity would occur through such generation of self-similarity through space-time. Thereby, this would be geometrically represented by connected fractal structures, stabilized  more uniformly by and through such forces. Therefore, these would be  conserved and hence  adaptive structures. Such interconnected fractals would represent a Principle of Universal Correspondence. This Principle would be applied to the dynamic drive for maximum force uniformity on various, respective levels composing the different organizational scales of physical phenomena. And this would involve the corresponding, similar behavior of these different scaled phenomena by means of such forces. The consequence would be progressive, dynamic stability through all physical scales and their dynamic geometries, and the corresponding means to effect such.

    In 1968 and 1969 publications, Paul Lieber described such a Principle operating in connection to a dynamic of maximum uniformity in non-uniformity and the universal, physical constants. Forces or their non-uniformity in magnitude were seen as an aspect, or manifestation, of the non-uniformity of a manifold (or plenum) that ontologically featured impenetrability. As Paul Lieber described, this non-uniform impenetrability is the essence  of forces and their non-uniform constraints. Impenetrability is conveyed by the forces. It enables the constraints of the forces. From the present perspective, such conveyed impenetrability would allow for their geometrical or architectural, force-structuring and patterning. Such would be guided or enabled, via plenum or space-time impenetrability, by an inner, generative template reality seated, with the impenetrability, towards  such architectures progressively having greater  force uniformity within non-uniformity, with ensuing progressive stabilization of such phenomenological architectures. And this would be occurring, generatively, through different self-similar scales of space-time. This generative, inner guidance would be reflected by the dimensionless components of the universal physical constants. As Paul Lieber noted, the increase in dynamic uniformity is the reduction of non-uniform constraints or forces within  physical and biological systems, independent of scale or level, with the consequent progressive stabilization, and hence, the generation of the very constancy of the systems,  also independent of scale, from the quantum level  at the micro-scale to the cosmological level. 

     Progressive stabilization, and thereby a manifesting constancy, in nature is realized at all levels through the forces, as noted by Paul Lieber. Constancy and specificity/diversity in nature could not exist without the forces and their conveyed impenetrability. According to Paul Lieber, the dimensional physical constants represent, mark and guide in corresponding ways this universal process of dynamically-based constancy in specificity/diversity through all levels of reality. Stability of states of matter in nature is not only ascribed to the quantum constant, Planck's constant, but to all the dimensional constants.  Constancy or stability within all levels of nature is ascribed to the dimensional physical constants operating through the forces and their corresponding patterns at different levels. This exemplifies the Principle of Universal Correspondence of dynamical processes or dynamic geometries through different scales.

The Avogadro constant would reflect and define a structural correspondence of the micro-atomic level to the macro-chemical level and be the inner unity and driver of that correspondence. The speed of light constant, c, would also be involved in an universal correspondence of other physical phenomena described in the Special Theory of Relativity, as noted by Paul Lieber in unpublished notes: In this regard, e/m = c² , which follows from e = mc² , indicates that variations in energy correspondingly generate variations in mass, and that this correspondence of variations is always constant or uniform, that is, c² irrespective of the scale of existence, from the quantum level to the cosmological level. It is a universal correspondence. In such generation of variations does constancy arise or is necessary for such constancy to manifest or arise, irrespective of scale and time. Such constancy manifested via corresponding variations through various scales is also a manifestation of unity in mass-energy, its conservation, which binds their variations together correspondingly through all scales and times, that is, through all scales of space-time, and thereby universally. In this situation, c would also appear to operate as a transcalar constant through all scales of the phenomenon of mass-energy. And being  parameters of c, so would Q^-1 and π.

 The persistence and the regenerational support of force through space-time, enabled through plenum  impenetrability, as implicit in Paul Lieber’s cosmology, would be the necessary enforcer of constancy or stability within the universe, its designs. And such persistence would enable the universal constants to guide and execute such constancy in different ways in different designs or structures, giving such, stability. The conservation of mass-energy, through its different forms, variations and scales, would be a manifestation of constancy through the constant persistence of force in space-time guided by the universal constants, its universal correspondence through different scales of space-time.

    "Every aspect of nature, including therefore such phenomena which by convention we refer to as classical, bears in this sense universal and complete correspondence to every other phenomenological aspect of nature, be it classical or non-classical [such as quantum mechanical and atomic.] By this thinking every natural phenomenon, classical as well as non-classical, is in effect a micro-cosmos of the universe " (P. Lieber, 1969), and of each other.

    In a written anticipation of this scale-free dynamic process in a 1961, unpublished article, Paul Lieber describes a variational principle for the hydrodynamics of viscous fluids.  According to this principle "vortex and spiral motions are indeed preferred in non-uniform flows."  Such motions  or flows are a generating uniformity in non-uniformity, and "the measure of [their] uniformity is maximum for real flows." This means that hydrodynamically a vortical or spiral pattern of motion or flows represents a maximum  uniformity of forces in a non-uniformity of forces within the fluid's motions of an integrated, cohering totality of molecules. This coherent pattern, vortex flow, as an accommodation to non-uniform  stress or force in a fluid, would apply to (and unify) all hydrodynamical and phenomenological levels, especially to coherent, cooperative, biological phenomena, as Paul Lieber noted.

    Part II: The Biological Dimensionless or Trans-Dimensional Constant in Dynamics, Fractals and Reality

We have seen the golden ratio or Q as defining or representing a common vortically regenerative, template-defined, component or manifesting factor within or implicit in all the dimensional universal constants of physics. These respective constants deal with or address specific physical situations and the specific forces endemic to those situations. Yet, such constants also refer to and depend on a common regenerative factor or dynamic patterning. This regenerative factor is template-based within the plenum. It is a-specific and trans-dimensional, but nevertheless, it is inherent within all specific physical situations, enabling their adaptive stability. Paul Lieber (1968, 1969) demonstrated that the dimensional physical constants mark or represent the accommodating, adaptive nature of forces in specific situations irrespective of the types of forces involved. Forces enable and promote adaptation of systems through the generation of stability and implicit constancy in all levels of existence.

   This accommodation has geometrical-dynamical constraints in and between various physical and biological systems. That is, as noted, the systems display a drive to achieve a maximum degree of force uniformity or completion within and between themselves. This would occur under or within the constraints of non-uniform forces or stresses, present within and between such systems. The physical constants would mark this constancy of the dynamic drive in various situations, including biological, to achieve a maximum uniformity of force within a non-uniformity of force or non-uniform constraints or stress. And consequently, this would lead to a maximization of the degree of stability within and between the systems, enabling the accommodation and conservation of such within a context of stress.. The golden ratio, Q , or its reciprocal common to all these dimensional constants, would mark or define or "guide", geometrically-dynamically-physically, how this is achieved or enabled, the effective avenue of the "go of it."

     Biological processes or living systems clearly show this. In bud development of plants, the buds develop in such a way spatially with respect to one another that there is likely the lowest degree or magnitude of mechanical pressure or stress between themselves. (See Posamentier and Lehmann, 2012.) This manifestation of a low degree of stress between buds is due to the constant angle of divergence between them. A component of this angle of divergence is the golden ratio or Q, as can be seen: 360^o/Q² equals 137.5. This  constant angle of divergence, 137.5^o, also referred to as the golden angle, enables, according to the aforementioned authors, the maximum number of buds to develop in a small space without interfering or inhibiting each other's development that would otherwise occur due to a high, inhibiting mechanical pressure between those developing buds. The generation of this golden angle prevents the generation of the inhibiting, high degree of mechanical pressure between structures within the small space. It is likely that this low degree of physical stress or force, its low magnitude and direction, will be found to be uniformly displayed or manifested between all specific, developing buds. (Numerically, this golden angle constant is equal to the inverse of the fine structure constant. See Lieber, 1998a for the significance of this. View PDF.)

     One can interpret this inhibiting, high pressure as being non-uniform, thereby a non-uniform stress. In this regard, the golden ratio or golden angle manifests and enables an adaptive and stabilizing process that would otherwise be greatly constrained or inhibited through, non-uniform, high stress. Moreover, in terrestrial plants having this golden angle between specific developing buds also enables these buds to achieve the maximum exposure to light for essential photosynthesis. Hence, the maximum uniform display of a low degree of mechanical pressure or force throughout a system of developing buds as well as a maximum exposure to light by means of the golden angle between the buds allows for different types of accommodation or adaptation, and thereby a stabilization of the living process.

    At a higher scale, the overall, growing arrangement of emerging buds from a plant stem or the arrangement of seeds within a sunflower with respect to one another is itself a spiral. This is a specific type of generating logarithmic spiral, whose inner ratio of growth dimensions is Q. This spiral, the golden spiral, is a logarithmic spiral whose growth factor or rate is Q per every 90 degrees of its turn or curve, irrespective of scale. Such growing curvatures would occur relative to an implicit origin within the plant. This particular developing spiral arrangement or pattern of emerging buds and seeds at this higher scale is referred to as phyllotaxis, and it appears that the golden ratio at the lower scale enables this arrangement. In the case of the sunflower seeds, one group develops along a given number of counterclockwise logarithmic spirals, while another group develops along clockwise logarithmic golden spirals of another number. The ratio of these two numbers of clockwise and counter clockwise logarithmic spirals, irrespective of the developing sunflower plant, is always Q. The same situation can be seen in various plants with regard to location of repeating structures making up the spirals, such as in the surface morphology of the pineapple, and the seed-arrangements of a pinecone, where the ratios of the numbers making up the different classes of phyllotaxis-logrithmetic spirals (e.g., clockwise and counterclockwise directions) are always equal to Q.

   These numbers occur within what is called a Fibonacci sequence, and adjacent numbers within that sequence have the ratio Q with respect to one another. This also demonstrates that at a still higher level of organization or scale, the golden ratio becomes again manifest in development, suggesting that the golden ratio is necessary for effective plant development, where forces are certainly and implicitly involved. In fact, it is pointed out again that the involvement of the golden ratio within the generating spiral arrangement enables the most efficient use of space (Livio, 2002), and probably of minimal force manifested uniformly through that space. Again, this may indicate a dynamic cause of phyllotaxis and the critical role that Q plays in such, especially as it appears to dynamically link coherently and with stability the different levels of developing organization, which appear to be self-similar.

    In this regard, a physical experiment strongly supports the involvement of Q in a physically organizing process: A dish containing silicone oil was placed in a magnetic field in such a way that the magnetic field was stronger at the dish's edge than at its center. "Drops of a magnetic fluid , which act like tiny bar magnets were dropped periodically at the center of dish. The tiny magnets repelled each other and were pushed radially by the magnetic field gradient. Doudy and Couder [the experimenters] found patterns that oscillated about, but generally converged to, a spiral on which the golden angle separated successive drops. Physical systems usually settle into states that [uniformly] minimize the energy [or magnitude of force used through space]. The suggestion is therefore that phyllotaxis simply represents a minimal energy [low magnitude force transferred uniformly through space] for a system of mutually repelling buds." (Livio, 2002.) A developmental patterning on different scales, guided or allowed by Q, would appear to only ensue in the maximization of a uniformly low magnitude of force through all limited space-time. In effect, the dimensionless constant Q appears to have enabled the most efficient, stabilizing, adaptive utilization of force in various biological and physical situations. Again, this is further illustrated.

   In other growth situations, the golden ratio or its reciprocal, defining vortical growth, might also represent geometrically or spirally the best means or avenues to achieving a maximum degree of low uniform stress within a growing biological system or organism, achieving maximal stability through space and time in the biological system or its dynamical architecture. For example, terrestrial plants, such as the angiosperms, produce branches (and leaves), and these appear to be produced or displayed in a self-similar, reduction manner, taking the form of a fractal. Let us consider the following in this regard: To achieve a maximum degree of a generating, reducing self-similarity, whereby all space between developing branches (and between developing leaves) are achieved with minimal contact between branches and between leaves, and thereby minimal mechanical pressure between the structures, the reduction fraction or factor of each branch produced would be 0.618 (the reciprocal of the golden ratio) the length of the branch from which it began as a bud. This reduction fraction would enable the production of the maximum degree of uniformity of branching within the tree or bush with the minimal of touching.

   This geometrical/architectural uniformity of branching, utilizing all space and generated through time and mathematically defined or allowed by the reciprocal of Q, could represent the maximum uniformity of low stress throughout the organism, that is, the tree. This fractal process based on or requiring the reciprocal of Q, which achieves through a reducing iteration such an adaptive, branching geometry, can be demonstrated by means of a very similar, fractal-generating procedure due to the reciprocal of Q, that is Q^-1. (See Posamentier & Lehmann, 2012.) Moreover, through this procedure, as the author found, triangles can also be constructed or denoted  or manifested from the lengths of branches on smaller and smaller scales, each of which triangle has an angle of approximately 31.6^o at smaller and smaller scales. The vertex of each of these angles marks the end of one branching structure and the beginning of another irrespective of scale. The tangent of this angle, which is the ratio of one branch's length to another at respectively smaller and smaller scales, is approximately equivalent to Q^-1, and thus Q^-1 becomes evident at smaller and smaller scales. Such a tangent, Q^-1, could also contribute to and manifest the architecture that best allows for a maximum, stable adaptation through various scales.

   Q^-1 would enable the generation or creation of a biological system of such a geometry wherein the maximum degree of a low degree of uniform mechanical force is achieved throughout the system. We have also seen where Q in the golden angle at one scale and in phyllotaxis at a higher scale also allows this. The geometry created by means of a self-similar, fractal reduction enabled or determined by the reciprocal of Q marks a situation where forces of low magnitude could be maximally displayed uniformly, that is, the maximal uniformity of low stress. Such could be adaptive as it gives a maximum degree of stability to the biological organism, be it a tree or a mollusc. Shortly, we shall see more examples where Q itself plays such a role.

    We see how the generation of a fractal geometry, enabled or allowed through a constant reducing factor common to the dimensional physical constants, could  also represent a dynamical, adaptive situation for biological systems. This adaptive, fractal process, whose constant, determining parameter or constraint is the reciprocal of Q, or of the golden ratio, also generates different, self-similar specificities, between which, more and more low level, uniform stress is likely enabled. Hence, the very generation of this self-similar specificity or diversity could allow for or provide more and more avenues for the creation of greater force uniformity throughout the specificities on and between the different fractal levels or scales. Hence, this would ensue in greater dynamical uniformity through greater specificity/diversity or non-uniformity, thereby greater stability in space and time.

    The different physical, dimensional constants represent different types of forces. But, due to the common, underlining and implicit constant that defines a common behavior of such forces, the various forces would also be governed by a fractal, dynamic drive to achieve a maximum degree of uniformity of magnitude within situations and periods, wherein such forces operate or are prevalent. This drive operates through either decreasing or increasing scales of the physical and biological realms. With regard to lower scales, as we have seen, this fractal, dynamic drive can have the constant of the reciprocal of the golden ratio, as only in this dynamical reducing factor, producing one type of self-similarity of increasing specificity throughout smaller and smaller scales, could ensue in a situation whereby a maximum uniformity of force is achieved throughout different levels of self-similar, specificity based on the reciprocal of the golden ratio. However, from the perspective of going from these lower scales to the higher, Q becomes manifest. It would appear that Q^-1 and Q represent together mirroring, regenerative drives towards dynamical uniformity within specificity. And from a global perspective or scale, these mirroring drives would appear to be occurring concurrently, completing one another during biological and physical development.

     Thus in development, the template of the golden ratio itself, 1.618 or Q, can, as  constant ratio  of vortical growth, also enable-guide or define an increasing self-similarity on higher and higher scales. This in fact generates a fractal or morphology based on or determined by a dilation factor or ratio, which is the golden ratio itself. By virtue of this particular ratio, or dilation factor, a growth is achieved that displays geometrically a maximum degree of uniformity within an increasing specificity or non-uniformity on higher and higher scales. This morphology or growth is displayed or arranged dynamically as a logarithmic golden spiral. And such a spiral dynamic would be displayed, self-similarly at various scales in the growth patterns and organization of various plants and animals, such as the shell of the Nautilus. And in fact, a 65 million-old fossil of a mollusc has a shape that closely resembles a logarithmic golden spiral, perhaps indicating that Q has been significantly relevant, if not necessary, to life for millions of years, an effective constant through time. In view of this, Q or what it reflects has had a very powerful, universal adaptive function.

   The logarithmic golden spiral and its constant features would also appear to be applicable to or define or represent, from various perspectives and analyses, including geometrical, the generative, adaptive designs of existence at various scales and dimensions, which scientists have denoted as physical and biological. This spiral, its features, though being an implicit, dynamic pattern within space-time, nevertheless, becomes accessible to us via abstract, geometrical analysis. The inherent constants or constancies through the logarithmic golden spiral become clearly evident, or explicit, via such analysis. And  also, via such analysis, they become very important in elucidating the nature and dynamic of those designs, which we define as reality or existence. As noted via analysis, making an implicit dynamic pattern, explicit, the logarithmic golden spiral increases or grows by a constant factor of Q over every 90^o of its curve at every scale within a specific set of different scales, from the smallest scale to the largest. That is, a logarithmic golden spiral becomes or growths wider or further from its implicit  origin by a constant factor of Q for every 90 degree turn it or its radius takes with respect to the polar coordinates. These would also be the implicit coordinates of a physical/biological coordinate system. In other words, irrespective of the scale or total size of the golden spiral, it grows by the constant factor of Q for every turn it makes over 90 degrees at its scale or size relative to its implicit origin and polar coordinates. As stated in Wikapedia: "In geometry, a golden spiral is a logarithmic spiral whose growth factor is phi [or Q], the golden ratio. That is, a golden spiral gets wider (or further from its origin) by a factor of phi for every quarter [90 degree] turn it makes."

  As another parameter  or feature defining this type of spiral: "If the radii vectors of a logarithmic spiral are in the phi proportion, the result is not only a pleasing spiral of singularly pleasing character, but there is the further feature that on any radius the sum of the distances between successive curves of the spiral equals the distance along the same radius to the succeeding curve." (Cook, 1914). The increasing, contingent, generated areas, bounded by these increasing radii and curves, would also be in the proportion of the golden ratio with respect to one another. Such generation would occur through time, creating a vortical structure through space-time. That is, if such areas (and volumes composed by such areas) represented space-time, their generation would give space-time and its phenomena a vortical structure defined through Q. Such vortically generated space-time or existence would also have other constant, connected geometrical features necessary to the architecture of space-time and its processes. Vortical generation would give stability to space-time or to its phenomenological features. Adaptation or accommodations would arise through such vortical or spiral generation towards stability.

  Pertaining to such, in its constant rate of logarithmic generation, the golden spiral, as do all logarithmic spirals, concurrently generates, as implicit extensions, equal angles of 60 degrees (and 30 degrees) with vertices along the concave of the curve, and the respective tangents and cotangents of each of these respective equal angles are always equal to approximately 1.718 at every scale within a given set of scales. In short, the logarithmic spiral also generates a constant growth rate of approximately 1.718 per unit rotation angle of the spiral radius per or within each equal angle. This constant rate of spiral growth (1.718) is indicated (or concluded) to be the constant logarithmic rate of growth of the spiral (Clifford, 1899). In other words, this  particular constant growth increase or rate per rotation is the approximate tangent of each of the equal 60 degree angles, and approximately equal to the cotangent of the 30 degree angles, which are generated along the concave side of the spiral curve. This concave side of the spiral curve is where the extremely small arcs (or their cords) of the spiral and spiral radii intersect to form the basis of the very small 90 degree right triangles with identical angles of 60 and 30 degrees along the concave side of the spiral curve. (Please note Figure S.) Triangles having identical angles with respect to one another are referred to as equiangular.

   Though a geometrical analysis, such likely reflects or makes evident further details of a generative process in existence or space-time, which creates constancy through change. More specifically, the unit angle rotation, implicitly, of the spiral radius-vector with respect to the implicit coordinates also generates the 90 degree angle of each of the equiangular or identical triangles, and thereby each of the equiangular triangles and their other angles of 60 degrees and 30 degrees. And which happen to be 60 degrees and 30 degrees, and which are equiangular or equivalent in all the triangles generated along the spiral curve. The respective tangents and cotangents of these two angles, whose respective vertices occur on concave side of the curve, are approximately 1.718. In effect, the generation of these equal angles along the concave side of the curve, constantly giving rise respectively and approximately to the tangent and cotangent 1.718, depends on the generation of the 90 degree angle, and thereby the tangent  and cotangent 1.718 also depends on such.

   The generation of the tangent and cotangent value, approximately 1.718, which is of the respective equiangular angles of 60 degrees and 30 degrees, per unit angle of radius-vector rotation, with respect to the implicit polar coordinates, always results in the exponential growth constant, e, which is 2.718, per unit angle of radius-vector rotation per each 60 degree (or 30 degree) equal angle generation and per each 90 degree angle of the triangles generated along and defining the concave side of the spiral curve. In effect, e or 2.718 represents the total growth-length or magnitude of the radius-vector of one unit length after it rotates through the 90 degrees of the very small right triangle, while concurrently describing or rotating  through an angle of one unit relative to the polar coordinates, that is, 1.718 +1 (Clifford, 1899).

   Adding the two components of this tangent or cotangent ratio, 1.718/1, or constant growth ratio, always give a scalar magnitude of 2.718. This also represents the total logarithmic growth-length or magnitude of the radius-vector upon completing 90 degrees of its rotation between the sides of each of the generating equiangular triangles, whose generation occurs through such rotation. The generation of e through equal angles, along the spiral curve, is enabled through this 90 degree rotation of the growing radius section or triangle side within and generating each triangle. This is a 90 degree rotation or the operation i with respect to a side of each generating triangle. A rotation of 90 degrees is equivalent to the rotation or operation i within a complex number, coordinate system. Also, note that the cotangent of the 60 degree angles is 1/1.718. This would also suggest that for every unit degree rotation of a vector-radius of one unit, with respect to the implicit polar coordinates, and 90 degrees with respect to the sides of the equal angles, it grows per a constant growth factor of 1.718, ensuing in a total length or magnitude of 2.718, or e. In effect, e becomes a constant based on 1 + 1.718.

 Clifford points out, through his analysis, that this constant rotation rate through 90 degrees (in the respective equiangular triangles) resulting respectively in e is also described by i in a complex number system, where the result of such generative rotation would be 2.718 (or e) to the power i, where i in the complex number system indicates an operation of rotation over 90 degrees. According to Clifford, this operation generating eⁱ represents a (another) constant logarithmic rate that manifests within a complex number context. This means that the generative rotation or operation i, through or per unit angle (such an operation also being a constant logarithmic rate i, according to Clifford), becomes e (or eⁱ ), the exponential constant. This would be a constant that structures intrinsically the logarithmic spirals inherently guiding existence. Thus, e or eⁱ is composed of or determined by a constant rotational growth rate, 1.718, manifested by i in the complex number system, characteristic of all, various logarithmic growth spirals. e, as itself a logarithmic rate ensues from or reflects another, underlying constant growth rate, namely 1.718 and the connected operation i. The association of e with a complex number system or realm may suggest that e, the exponential constant, and thereby a spiral generation based on such, reflect generatively a deeper substratum of existence, which is "imaginary" from our space-time perspective. It is through e, and thereby spiral generation, that a connection arises generatively between that substratum of existence and our own space-time existence.

  The generation or particular magnitude of e becomes contingent on this particular 90 degree rotation (or i ) over a much smaller scale relative to or associated with the generating curve, a scale involved in generating the equiangular triangles along and defining the curve (Clifford, 1899). This generation of e becomes another constant feature of the logarithmic golden spiral along with Q. Q would concurrently define the constant growth of the spiral over 90 degrees, with respect to polar co-ordinates referencing a constant radii ratio or proportion  implicit in the developing spiral system. And thereby this would also involve i at much higher scales. These are scales at 90 degrees are much higher compared to the scales of 90 degrees, and thereby i, at which the constant logarithmic rate, 1.718, underlining or ensuing in e, occurs. This occurrence or generation of 1.718 is through the generation of the equiangular triangles, whose generating hypotenuses, as cords, become, very nearly, the generating, very small sections or arcs of the logarithmic spiral curve, thereby at the scale of the spiral's curve itself.

In effect, constant generations of 1+1.718 (or e) through 90 degrees, or the operation i, within the chain of very small equiangular triangles present at exceedingly lower scales, and associated with exceedingly small concave sections of the curve, integrate as a totality to compose (or ensue in) generations of the constant 1.618 radii  proportions of 1.618 (or Q). This integration would be with respect to the polar coordinates, over 90 degrees, or  the operation i, at higher scales. In other words, this constant spiral generation pertaining to a constant, generative radii ratio or proportion of 1.618 over 90 degrees would be relative to, or associated with, the spiral's polar coordinates and origin. And this would be implicit with respect to natural processes involving the dimensionless and dimensional universal constants.

 This analytical information about the golden spiral points to a critical relationship between Q, e, and i, and one defined or reflected by an important equation (based on Euler's mathematics), whose deeper meaning for natural processes will be addressed shortly. In effect, the golden spiral being also a type of logarithmic spiral, and  also being an inherent reflection of physical and biological processes, would also have e and i as constant operational parameters. Moreover, this relationship between e and Q can also be seen as follows: e = Q^-1 + Q^-2 +1.718. This is so  as Q^-1 + Q^-2 = 1. This would indicate that two negative powers of Q also implicitly contribute to the logarithmic spiral of physical and biological processes, and thereby, these two dimensionless constants would implicitly be also within the universal dimensional constants of physics.

  Relevant to this, along with its deeper significance in nature becoming evident through a geometrical analysis, e is also an extremely important mathematical constant, and it shows up in calculations dealing with or describing physical phenomena, as would also be predicted from e = Q^-1 + Q^-2 +1.718. It was noted earlier that 1.718, as a contributing, generative basis for e, might also occur, and be seen through factoring, as another generative, dimensionless component of some other dimensional physical constants (Lieber, 1998a), including those to be discovered. Note that 1.718 is almost identical to 1.618, that is Q, which is also significant. In that publication, 1.718 was denoted as Q₂. Could Q (or Q1) and Q₂, as well as other dimensionless constants of growth, refer to features of the same, basic generative operation or situation within different sets of scales within existence or space-time. This would be where each scale-set corresponds to a different infinity, such as those described by the mathematician, G. Cantor, at the end of the 19th century? Could Q1 and Q₂ be applied interchangeably?

 The near identity of these two generative constants, Q1 and Q2, has an important meaning or significance, which as yet is not clear. Though, as we have seen, there are significant relationships between these two constants. Furthermore, there may be more clarification in this regard through considering information in the following paragraph. (Relevantly, also, see Table 1 pertaining to the generalized logarithmic equation and its representation of different constant growth rates in the turns of different logarithmic spirals. These constant rates of generation may also correspond to other dimensionless, biological constants involved in other natural vortical generations not based on Q1.) In view of the above, the constant 1.718 (Q2) can thus be seen as being generated along two different avenues.

 As noted, the logarithmic rate 1.718, which is a constant growth rate, results generatively in e, or underlies e, an example of constancy through generation. And most significantly, there is also another, clear relationship between e and Q, because Q^-1+ Q^-2 = e^2πi (Lieber, 1998a). This equation might refer to the generative and geometrical-inducing properties of a deeper reality or plenum, a type of fluid-like, ultra-matter that could underlie and pervade space-time and give structure to it (Lieber, 1998a). This plenum or manifold, imaginary from our space-time perspective, having the property of impenetrability (according to P. Lieber, 1961, 1969b), would be the  "imaginary" seat and non-uniform embodiment of the curvilinear forces arising and manifested in space-time via the geometrically-shaped field. Possibly applied to this deeper realm or plenum, the imaginary number, i or1i, the square root of -1, refers to an operation that defines an increasing, constant curving generation over an angle of 90^o in a complex number plane based on imaginary numbers composed of i. (Such a complex plane could represent a feature of the plenum.)

   This constant rate of curving generation over 90^o (with respect to polar coordinates in an intrinsic complex number milieu) at all scales would be represented by i through π/2 radians. Such could also be or correspond to the generation or manifestation of Q through the plenum, where Q manifests itself via as well in guiding self-similarly such curving, uniform forces in specificity over 90^o at all scales within an infinite, particular set of physical scales. Q1 would also represent a self-similar, curving regeneration over 90 degrees or i generation (operation) over another, particular infinite set of physical scales. Both constants may depend on a deeper constant, i. This constant might also be a feature of a universal template operating imprintingly and self-similarly through various set-scales of existence via these very defining, dimensionless constants. The relationships between Q, π, i and e, as displayed in the above, previous equation, can also be seen in the equation of the logarithmic golden spiral within a complex number system or plane on which a physical coordinate system could be based  (See Table 1).  As this equation indicates, the constant powers of e composing this equation of the golden spiral determine the respective distances, along the implicit radii, between the curves of this generative spiral with respect to its implicit origin and coordinates, and thereby its generative  ratio of growth, Q.

 And as noted, the dimensionless constant 1.718 would  also refer to or define the generation of the other constant, generative growth ratio manifested, as constant tangents and cotangents, along the inner curves of any logarithmic spiral. In this role, the  constant 1.718 would also give stable, generative configuration to all logarithmic spirals, and thereby, would give stability to the physical and biological processes enabled spirally through the operation of such a constant. Along with Q, the constant 1.718 would enable the inner spiral guidance of such processes to such stability. And this inner, logarithmic spiral guidance to the stability of physical and biological phenomena would be marked or reflected by the universal, dimensional physical constants. Yet, the constant 1.718 would enable all types of guiding, physically necessary, logarithmic spirals or vortices with (or having) various, constant growth ratios pertaining to implicitly increasing radii relative to implicit polar coordinates. And these would be various constant growth ratios that would include Q. The constant 1.718 would thus be also implicit in all dimensional physical constants, including those to be discovered. And thereby, such a constant would appear to be more universal and fundamental than Q, especially as Q arises through a logarithmic spiral configuration based or dependent on the pervasive operation of the constant 1.718, whose generation is manifested by i. Again, it is to be concluded that the constant 1.718 can be generated by means of different operations or avenues. This also contributes to 1.718 being a very fundamental constant of various avenues of constant growth.

   These constants, e, i, 1.718, Q, π, and collectively their relationships to one another, become manifest (from their seat in a plenum) through the consequent generation of the self-similar logarithmic spirals on and through all scales of existence (and their sets), and correspondingly, in and through various phenomena. This points to the operation of such dimensionless or transdimensional, universal constants explicitly and implicitly in the maintenance of the dimensional constants within various scales of phenomena, hence of the phenomena themselves in which the dimensional constants become manifest. The operation of the latter also points to their involvement---through the dimensionless constants---in the generation of a geometry of force that displays through and is defined or enabled by a logarithmic spiral, a maximum uniformity of curving force within specificity and diversity through various scales and implicit coordinates, and hence an ongoing generation of stability through those various physical scales.

    In other words, it is thus likely that, structured via the templates of the dimensionless constants, this vortical geometry (or vortical architecture) of maximum uniformity within specificity also represents, defines, and allows a maximum uniformity of forces within diversity (or various non-uniformity) on all scales or levels of organization through space-time, from the very smallest to the very largest. The golden ratio and its reciprocal would appear to be those dimensionless constants that, within a spiral or vortical configuration, enable or determine, or through which, a maximum uniformity of force of various types, such as mechanical and magnetic, can be achieved throughout different levels or scales of specificity and diversity. And, in so doing, this process would give stability through those different scales, and thus be adaptive for natural systems or natural designs, such as biological organisms. The feasibility of this view or hypothesis can again be demonstrated experimentally with physical phenomena.

    In an experiment involving the changing spatial relationship of ferromagnetic balls being added in a magnetic field, a regular spiral pattern based on Q was generated within the changing geometrical arrangement of those balls. (See Posmentier &Lehman, 2012.) This might also suggest an arrangement of magnetic forces between all these balls that can only achieve a maximum degree of global uniformity or stability by means of a spiral or vortical geometry enabled by the golden ratio. As pointed out by Posamentier and Lehmann (2012),"this pattern building [based on the golden ratio] has also been observed in many other non-biological systems." Predictably, these could be systems where the dimensionless constants appear to become evident.

     In fact, quasi-crystals display a geometry of inter-connected and partially over-lapping decagons in which all space is completely used in such a manner that a maximum uniformity of pattern or symmetry is created compactly throughout all space on different scales of the crystal. The geometry is based on Q throughout the geometry and could not have arisen without it. (See Posamentier & Lehmann, 2012.) It is likely the geometry is sustained or manifests itself by forces in uniform magnitude throughout the crystal, indicating that the forces sustained or manifested the geometry by means of Q's influence on that very geometry. And it could have only done so if the forces emerging from the crystal themselves eventually displayed configurationally a maximally uniform force magnitude throughout the crystal due to the operation of Q on the crystal's geometry. In effect, within a natural substance, Q could have guided or enabled or determined---perhaps via a type of geometrically-mediated, global imprinting---the generation of a maximal, stabilizing force configuration throughout the crystal and through its geometry, a force configuration manifested by a Q-enabled geometry.  In short, Q would define or guide the crystal's geometry of forces, and those forces retroactively and stably would maintain or enable that very geometry by means of Q's guidance. By means of Q, the geometry of the crystal  would manifest the forces and their patterns, and the forces and their patterns would manifest the geometry. Through this, stability, and thereby constancy, would become manifest and enabled through the dynamic of regeneration represented and guided by the dimensionless biological constant.

    Significantly regarding the operation of a Q based geometry and force in genetics, a given cross-section of the DNA molecule making up the genetic material is also a decagon in which Q is represented. (See Hemenway, 2005.) Again, this might suggest a maximum degree of patterning, uniform force throughout the DNA molecule for its stabilization, a stabilization enabled by Q, and a stabilization that would be needed for a stable or constant inheritance of the gene. Perhaps, also contributing to this stabilization is the ratio of the angstrom distance of one complete turn of the DNA molecule to its diameter, which according to some reports is 1.618 or Q (34A/21A). (For example, see Hemenway, 2005.) Other reports have the diameter as being 20A. Even so, the ensuing ratio of 1.7 is not significantly different from Q. When DNA is in less than a stable state, as when it is under stress, it can undergo mutation.

    In this regard, when hypermutation rates within genes in bacteria due to environmental stress are divided by spontaneous mutation rates of such genes under no stress, the factor Q (or its various forms such as Q²) always appears as a coefficient. This analysis was performed by the author on his own hypermutation data (Lieber, 1998b) and on the mutation data from different researchers investigating hypermutation. As the author pointed out in that publication, hypermutation apparently becomes a means to re-stabilize the genome following a non-uniform stress. Thus, Q also appears to be an indicator of this dynamic. In this connection, one might wonder that on the scale of adaptive evolution involving extremely high mutation rates, Q or its forms (exponential powers thereof) may have also played a guiding role, leading to the stabilization of life at one of the highest of scales. That pattern of evolution is represented as a complex branching tree, where a maximum degree of uniformity in specificity or non-uniformity has been generated through space-time. The branching patterns of living trees and bushes replicates in a self-similar pattern on a lower level or scale the branching pattern of the evolution of organisms, and a constant common to each scale could be Q or Q^-1, as is likely a maximum uniformity of forces within specificity common to each level of these organizations, and also probably patterned or guided by Q. Q could represent a true constant on the scale of evolution. The logarithmic spiral, displayed by many vortical hurricanes and vortical galaxies, demonstrates the operation or guidance of Q (and implicitly i and e) on the pattern of forces generated within and through the shaping of these systems also at the highest of scales.

   From the preceding analytical accounts, we see how or why these implicit and explicit dimensionless (or trans-dimensional) constants, such as i and Q, compose and underlie in different forms and ways the various, universal dimensional constants of physics, and, in so doing, playing a significant role in physical and biological phenomena on various scales, and hence the deep connection between force and its vortical generation and the dimensionless constants. Namely and more inclusively, the dimensionless constants, which include primarily and explicitly the various forms or powers of Q and Π, and, also implicitly, the constants i and e, the exponential constant, collectively represent, define and enable, through their templates, a constant, universal dynamical drive to achieve a maximum degree of dynamical uniformity in specificity and diversity within and between all specific scales of physical and biological systems or phenomena.

   Such a universal drive would be through the fractal creation---primarily defined or enabled by the golden ratio and its reciprocal or powers---of those very specific systems on all levels of fractal organization.  Through the explicit, primary and necessary presence and application of this underlining, biological dimensionless constant, Q, or its forms, could a maximum uniformity of force be achieved in various systems or phenomena, and hence their maximum stability or integrity. In this situation, the other dimensionless constants would appear to define and represent implicitly the constant, contributing, curvilinear or vortical generations involved, thereby behaving in a subsidiary though significant role in achieving a maximum, adaptive stability.

   The deeper implication is that the template of the golden ratio, or what deeper organizing template that template reflects, applies to all particular levels or scales of reality, from below the quantum level, where six, hidden, new curled dimensions might be present in addition to the four dimensions of our reality, to the cosmological level. Physicists conjecture in various publications that there may be ten dimensions to the universe or physical reality. This might be denoted or indicated subtly by the repeated occurrence of π² (ten) along with Q in the expressions of the dimensional physical constants. This further implies that there is a universal organizing principle or template, whose features are represented or defined by these dimensionless constants involving Q and π² , operating on different levels or scales of organization, probably enabling a maximum uniformity of force within growing specificity, even at the quantum level or below. If these proposed dimensions are ever demonstrated experimentally, it is predicted that Q will also become evident as a parameter.

   The Planck length or scale, which is Q x (π² )^-35 meters, and which is derived from three dimensional constants, would appear to show that Q operates or enables patterned dynamics at one of the smallest detectable lengths or dimensions. That is, this operation of Q would be at an extremely tiny micro-scale of reality, where the effects of gravity force-fields, their geometry, merge or fuse with quantum phenomena or states. And, in so doing as Penrose (1994) argues, the different gravity-fields of different, evolved, superimposed quantum situations or states or alternatives, which are represented by an algebra based on the imagery number i or 1i, could also merge or resolve in a stable manner, producing one, reduced, non-superimposed, localized, dynamically stable, quantum-gravity system from many possible ones.

   According to Penrose, it would be the incompatibility of these different gravity-fields, their geometries, with one another, and a dynamically driven accommodation to such, that would determine the resolution towards the reduced, stable quantum state, that is, the collapse of the unstable, superimposed, non-local system into a reduced, local, dynamically stable system. Might this stability be based on a uniformity and fusion of forces defined by a geometry structurally defined by Q, and whose stabilization through Q might eventually be made evident through experiment? Also, the persistence of the superimposed quantum states through evolution could involve a spiral regeneration of force through time, a regeneration defined by the imaginary constant i within an algebra of complex numbers As Penrose points out, such an evolution represents a determinism at the quantum or micro-level of existence, and this evolution of superimposition can only be described through the algebra of complex numbers.

     This process of progressive stabilization, the ceasing of superimposition, might even occur in a self-similar manner through and by means of an increasing fractal whose geometry is based on Q and the imaginary number or constant, i. (There is a very close regeneration-correspondence between Q and i as pointed out by Lieber, 1998a.) Perhaps, such stability of states would also occur concurrently at an extremely small scale connected or opening to the six hidden, curled dimensions on and of even smaller scales within fractals, whose very generation could predictably also be defined by Q, i, and π. Through  reality would appear to be a complex fractal (or fractal process) composed of adjacent fractals within fractals. This complex fractal or fractal process would be vortical in configuration through self-similar, logarithmic golden spirals reflected or defined by Q. Specifically, such dynamically self-similar spirals would be contingent on an underlining, constant, growth parameter reflected by Q or its reciprocal. (See  Figure 1 and Figure 2.) Perhaps, this fractal feature running through reality could also be described by an analytical geometry of complex numbers, as well as by π, e and Q. This fractal feature or process would not preclude other phenomological geometries from emerging, but would appear to enable such, also through vortical regeneration.

   This constant, dimensionless, parameter reflected by Q, and  by the other dimensionless constants, could thus  enable the morphogenesis of this universal fractal situation and the self-similar, uniform configuration of forces that would sustain it stably through all various scales. This would occur by means of a universal projecting template, whose facets would be universally featured, expressed and templately defined through Q and the other dimensionless constants. Such projection would be via imprinting through all scales. It would be a morphogenesis,  occurring through such projection, that enables and represents maximum inner, dynamic, stable accommodation to stress within and between all scales of itself. Might some day will the likely inherent logarithmic, vortical structure and vortical dynamic of reality at all scales become experimentally demonstrated, even at the quantum level. It is predicted that this will be the situation. In a limited way, this has already occurred.

     One way this vortical process, structuring reality, could be represented mathematically is with the following equation similar to the one in Table 1: F_u [r(ϴ)] = e^iθlnΦ/π/2 where F_u refers to uniformity of forces generated over various scales within any vortical, self-similar structure defined by Q (or Φ), π, i and e, the symbols defining constant, exponential and spiral generation through change, that is, a constancy through change or uniform, vortical action. Through vortical action, or rotation through the vortical helix, regeneration occurs. And such regeneration creates constancy through change via the forces, and thereby, stability through change.

Perhaps, the equation, itself a type of constant or universal representation through different scales, also refers to the actual, self-similar unfolding of all the possible vortical structures of force that could exist superimposed, a superimposition that could be defined by the algebra involving i. Regarding these vortices, the boundaries between the adjacent, unfolded vortical fractals could represent the discontinuities on the quantum scale, but, inclusively at a higher scale, these boundaries could have themselves the shape of intersecting logarithmic spirals of curved lines of force emerging from the non-unformities within a generative plenum. In effect, relevant to quantum mechanics, discontinuities of energy or force could emerge from and be defined by the intersecting, spirally curvilinear continuities of geometrically enabled or mediated force via Q. A unity is brought to bear through different structures and levels of existence.

                                                                         III.  Epilogue   

Many computer simulations of various fractal morphologies, visible on screens, have been generated using a basic iterative or feed-back loop algorithm (with exponents) involving the complex number plane based on the imaginary number, i. Many of these fractals take on the intricate and complex shapes of various integrated spirals or vortices. Others closely resemble complex, branching aquatic plants and small, aquatic invertebrate animals. (See Pickover, 1990.) This iteration is involved in the generation of the self-similarity on various scales of these vortical and biomorphic fractals. Such iteration or looping or twisting, producing, engaging and connecting various scales, would be a necessary, significant feature of regeneration, especially of biological regeneration. As pointed out earlier by this author (Lieber, 1998a), the biological constant, Q, the golden ratio, or powers thereof, defines or reflects a self-similar process of regeneration through forces on various scales by means of a repeated imprinting within and through the space-time geometry of physical and biological reality.

     The very computer generation of the various fractal morphologies use and depend on electric and magnetic forces and the electromagnetic energy of light for the display to be visible. Though computer programs enable the generation of the fractals, such programs must be designed in such a way whereby the dynamic process of regenerative-iteration through different scales, via those forces and energies, has to take place, in effect duplicating or representing on a much smaller scale what is occurring in nature. In the natural world, the regeneration of self-similarity through iteration is defined or enabled by Q.

     This regeneration, spirally manifested and defined by Q, would also become the manifestation of a projective template, a type of symmetrical imperfection within an underlining plenum or substratum to space-time, creating imprinted non-uniformities within this plenum and extending as patterning, guiding forces into space-time via vorticity. In so operating, this imperfection would self-similarly modify and define a space-time-field geometry and would manifest itself transcalerly through its evolving imprinting on the underlining plenum and into space-time. And, in so doing, would create and projectively evolve progressively stabilizing and guiding forces on all  space-time scales within phenomena.

   This could be a template that might be considered an inherent, universal program or principle and a source of a guiding mathematics, as geometry. This would be especially a force-involved geometry, which would be patterned and mediated by and through the dimensionless constants, such as Q. Such dimensionless or trans-dimensional constants would be the guiding avenues, through guiding forces, that would enable the universals of the inherent template to extend into our existence and give dynamic structure and form to it. Relevantly, the physicist, David Bohm, spoke of a theoretical implicate order that underlies and enfolds our reality. According to Bohm, this implicate order unfolds, creating and shaping our reality, which he referred to as the explicate order. (See Peat, 1996.)

                                                               IV. Concluding Remarks

    One may ask whether such a template/program/principle exists. Is this a valid scientific hypothesis that can be tested? The information presented in this article, much based on experimentation and mathematical applications, suggests the feasibility of such a template with geometrical properties being present, which may further indicate the existence of an inherent mathematics within the universe that gives shape indirectly to reality. The physicist and mathematician, Roger Penrose (1994), does argue for independent, eternal mathematical expressions and rules within the universe to which our minds have direct access, many of these having been used in physics. Our minds being a part of the universe and seeking and engaging eternal mathematical expressions within reality would in itself be a type of experiment or scientific test. Moreover, newly discovered mathematical expressions, especially with new types of constants, could suggest the existence of new types of phenomena or new relationships within known phenomena, as has been the case in the history of science. These predicted, new physical phenomena may predictably make evident new, dimensional constants dependent on Q or its various forms.

      Yet, what about the traditionally empirical or scientific method of testability that has been so successful? At this stage of scientific development, the existence of such a template may not be directly testable due to the current limitations of our scientific apparatus or technology. However, with the development of new scientific technologies and approaches via the application of mind, the hypothesis could very well become testable. In fact, there may be an approach to such an experimental test through the known organization of the microtubules composing the neurons of the brain. The organization of the protein components of the microtubules, which make up the functioning cytoskeleton of cells, is based on numbers having the golden ratio with respect to one another. (See Penrose, 1994.) As Professor Penrose points out, various scientists argue that this particular organization, which is based on the golden ratio, enables the microtubules to function more efficiently through changes in their conformations mediated by electrical forces, behaving as information processors. As Penrose further shows, these microtubules are very likely required for higher consciousness, which he says could manifest itself as a quantum coherence on the macro-scale throughout all the interconnected microtubules of all the neurons of the brain.

       As the golden ratio, the dimensionless or trans-dimensional biological constant and an apparent template in this situation, is essential for the organization within the microtubules, is it not possible that the template of the golden ratio can imprint itself ---via the dynamics shaped by this organization---on this coherence, our minds? And that this imprinting could be demonstrated? And through this imprinting, could we not have grasped its deeper significance and universality, a universality which would also suggest an imprinting of a template represented by Q onto our consciousness, our minds? Perhaps, through a further investigation of such microtubules, and their enabling of consciousness, could such an imprinting-template be accessed or demonstrated, perhaps holographically projected outside our minds.

            In  view of this, such testability could be feasible at some time. At present, this may seem to be a difficult if not a nearly impossible task. Yet, the history of science demonstrates how the development of new technologies and approaches enabled the testing of important theories, which before seemed impossible to test. Thus, it should remain for the future to ascertain whether or not such a template exists, but it will be a determination that ultimately depends on mind creatively connecting to and using a deeper reality or existence, perhaps one reflected through a multidimensional geometry based on and allowed through the eternal, transdimensional, universal constants Q, e, i and Π. This should be the source of our motivation and courage to find new truths.

                                                V.  Further Thoughts about Predictions

    Does physical theory predict the existence of the very dimensional physical constants of nature? According to Paul Lieber (1968), the very generation of stability and constancy within nature through forces would indicate the necessary existence of the physical dimensional constants in physical phenomena and their representation in a mathematical description of such phenomena. As he argues, the Special Theory of Relativity demands that the speed of light be a constant. The deeper implication of this is that the Special Theory of Relativity would have predicted the constancy of the speed of light, even if such constancy had not been demonstrated before. In the same article, Paul Lieber shows that the stability, a type of constancy, of the states of matter within quantum mechanics demands the existence of a constant such as the quantum of action, Plank's constant. Again, this implicitly predicts the necessary existence of such a constant had it not been demonstrated before the stability of the quantum states of matter was discovered. In view of this, it is likely that the other dimensional constants, such as the charge of the electron and proton, could have also been predicted.  The physical dimensional constants represent or define the deep connection between constancy or stability in nature and the forces, such constancy and stabilization depending on the forces and their patterns.

    Implicitly, the dimensionless biological constant or its forms should also be predicted if these compose the physical dimensional constants. As it appears that this biological constant defines or represents a vortical regeneration that gives enhanced stability, and thereby constancy, to physical and biological processes or phenomena at various levels of organizations, this dimensionless constant Q can also be predicted as being demonstrated through such phenomena, especially processes having a vortically structural dynamic. The very constant electrical charge of an electron (and implicitly of a proton) demands the predicted occurrence of Q as a necessary structural representation of this charge. Why would this be the case as we note the direct evidence of Q in this constant? As pointed out (Lieber, 1998a), there is evidence that “particles” such as electrons and protons have an asymmetrical, vortical structure, where one charge, say negative, occurs when the vortex is asymmetrically left-handed and the opposite charge occurs if the asymmetrical vortex is right-handed, or vice versa. In other words, electrical charge is dependent on complementary, asymmetrical configurations, that is, mirror images of the respective vortices. As pointed out in that article, such vortices suggest an inherent hydrodynamic nature of reality on all scales, including the quantum mechanical. Based on the vortical morphology of matter on the quantum level, one can predict that a constant of matter on that level would be directly represented by Q, which also defines the vortex of a logarithmic spiral and its generation of increasing stability from the quantum level to cosmological level.   

Through vortical action, or rotation via the spiral, regeneration occurs. And such regeneration creates constancy through change by means of the forces, and thereby stability through change. In unpublished notes, dated May 3, 1978, Paul Lieber points out that rotation through a helix is regeneration, which resolves constancy with change in various phenomena, such as fluids in motion. And such helical rotation is enabled and supported through impenetrability, perhaps ultimately of an underlying plenum or manifold, whose non-uniformity becomes manifested as forces in space-time. As the author has illustrated in different ways, it is the patterns these forces manifest and evolve which is contingent on the dimensionless constants.

     It would seem that Q and its forms, as well as other critical constants such as π and i, represent and manifest a template within the plenum that, through these constants, projectively guide and enable, via imprinting, the vortical, self-similar generation of those force patterns. Such generation would allow for a maximum uniformity of force within non-uniform force magnitudes throughout all physical scales and situations. This would  achieve through such uniformity, dynamic completion, and in such completion, stability. And thereby, such a projective template into space-time would enable, through those constants, a vortical, hydrodynamic drive or conserving regeneration towards maximum stability and dynamic completion on all physical-temporal scales. Through such a transformation process, a conservation of physical integrity or physical system, and connected physical laws, would be achieved or enabled continually, and hence what physicists refer to as physical symmetry. This would be through all scales of reality by means of vortical regeneration. This symmetry as continuity of system integrity or its dynamic maintenance would reflect a constancy through all spatial-temporal scales via vortical regeneration enabled by Q and the other constants related to the universal template.  Might those enabling constants in effect be extensions of such a universal template, by virtue of which, those enabling constants such as Q being templates themselves? (See Figure 3, Figure 4, and Figure 5. The image in Figure 3 could represent a vortically-structured reality emerging biologically in space-time from an underlying plenum-field through a template projection manifested by Q's guidance.)

   As this article has argued for the existence of an enabling, underlying and implicit dimensionless (or trans-dimensional) biological constant, which manifests within all the dimensional physical constants, and thereby provides evidence for its existence, hence linking or fusing the physical constants, this article has not only predicted the existence of such a biological constant and its forms, it has shown their existence is very likely, especially their role in achieving maximum stability, and hence maximum accommodation. Also, had this dimensionless or trans-dimensional biological constant been demonstrated in physical phenomena before the discovery of the dimensional physical constants, the latter might very well have been predicted because of the former.

Though, other enabling, biological constants analogous to Q might also be found. These would be respective growth constants per 90 degree turns of respective logarithmic spirals other than the golden spiral. These biological, growth constants, analogous to Q, and their defining logarithmic spirals would geometrically represent and pattern further vortical, generative features of projecting realities on all levels, some yet to be discovered. And thereby could manifest or determine new physical constants yet to be elucidated. These would be realities or systems, guided by constants, vortically developing towards a maximum dynamic uniformity or completion in non-uniformity And thereby, this involves  increasing  the stability, integrity and connected adaptiveness of the systems.

 Such completion would involve the generation of completing forces, as complements of force. And such complements of force, adhering or connecting to the non-uniform force configuration, would ensue in such configurations being completed or uniform in force magnitude. Through the currents of vorticity, would such complements of force be continuously generated and drawn to their complementary force non-uniformities, which vorticity concurrently also generates. Such generation of vortical currents would draw on an underlying, non-uniform plenum. The non-uniformity within the plenum would be due to a nexus of intangible templates or connected forms within and generating through the plenum. And these connected templates would make their (or its) existence known via (and into) our realities, constantly, through the dimensional and dimensionless, universal constants.

 It is predicted that if physicists and biologists seriously consider the existence and enabling operation of a biological constant marked by Q, or analogous biological constants, incorporating it or others into their approaches, a truly unified view of reality may ensue. This unified view would show a drive towards a maximization of stability  and dynamic completion on all levels of physical reality or physical scales. This would be a unification through an enabling, constant dynamic pattern reflected by Q. This would be a universal, trans-dimensional constant of particular vortical regeneration, through which, the known universal, physical, dimensional constants appear to arise and endure.

   In 1969(b), Paul Lieber was thinking along similar lines with regard to the universal dimensional constants of physics when he wrote: "These constants, I believe, are the universal constants of nature and therefore in particular of the life process.  It is in these constants and in what their existence manifests that the processes which we arbitrarily ascribe  to the inanimate and animate worlds merge, and where we must search for their synthesis and thus their comprehension." And through a concurrent investigation of the universal, dimensionless biological constant, and of similar constants, such a universal comprehension will be achieved. This would be a comprehension that would conceptually grasp in total, and hence enumerate completely, the drive for dynamical completion through out the universe. Such dynamic completion would be the universe's accommodation on all scales within and to itself.

                                                    Michael Lieber, February, 2015

                                Amendments were made during November-December, 2024.

 

                                                                          Table 1

Some Dimensional Physical Constants Exhibiting or Manifesting a Dimensionless or Trans-Dimensional Biological Constant, Q (and its forms), Equivalent to the Golden Ratio, 1.618 and The Dimensionless Geometrical Constant, Π (π ) or Pi. Two dimensionless, physical constants are also included.

The electric charge constant of the electron: Q x (Π²)^-19 coulombs

Proton/electron mass ratio: 3Q^-1 x (Π²)³

Mass of the hydrogen atom: Very close to Q x (Π²)^-27 kg

Kinetic energy of a V volt electron: V(Q x (Π²)^-19 J

Gravitational constant: (Π²Q^-1+ Q^-1) x (Π²)^-11 m³ kg^-1 s^-2

The quantum of action (Plank's constant): 4Q x (Π² )^-34 Joules-second

Plank's constant is also: (2Q + Q^-1 + Q^-2) x (Π²) electron volt-second

Velocity of light: 5Q^-1 x (Π²)⁸ meters per second or 1/2Π²Q^-1x (Π²)⁸ meters per second

Avogadro's constant: ∏² Q^-1 x (∏²)²³ per mole

Boltzmann constant: 2Q x (∏² )^-24 cal/^o C or 1+Q^-1/Q x (∏²)^-23 joules per degrees Kelvin

Bohr radius of the atom: 2Q² x (Π²)^-9cm

Nuclear magneton: (Π²Q^-1- 1) x (Π²)^-27Jm²Wb^-1

Compton wavelength of the proton and neutron: 6(Q + Q^-1) x (Π²)^-14 cm

Fine structure constant: 12Q^-1 x (Π²)^-3 or (2 + Π²)Q ^-1 x (Π²) ^-3  

^{Inverse of the fine structure constant:} 360/Q²

^{Numerically, this is equal to the golden angle constant within phyllotaxis. See Lieber 1998a for the significance of this.}

Plank's length: Q x (∏² )^-35 meters

8Π (8π) is a component within a compact expression, a tensor equation, (shown in various publications, such as in the appendix of the publication, Hyperspace, by Michio Kaku, published in 1994, and in Wikapedia) of Einstein's field equations for General Relativity*.  Significantly, 8Π = 4Π²Q ^-1   =  (Qπ)²

^{This shows that gravity and mass are dependent upon constant, regenerative parameters, namely}  Π (π ) and Q.

*The follwing tensor equation represents the ten Einstein field equations of General Relativity:

G_{uv +} g_{uvɅ  =} 8πG/c⁴ T_{uv    Ʌ is the cosmological constant. T defines the energy-mass tensor between various points uv in the space-time field, and which determines space-time curvature between various points uv. g is the curvature tensor between various points uv within the space-time field. G is the gravitational constant.}

In physics, the equation or expression s = 1/2gt² defines the distance through which a body falls due to acceleration by gravity, where g is the constant of acceleration and t is time. It was shown that the integral of this equation is 1.62 space-time or Q space-time (Lieber, 1998a). This defines or represents a conical section or region or area of space-time structure.  Composing such an area-structure, space-time would be squared.  One can transform this region or “area” into a volume in a coordinate system, where the volume is shaped as a cone with a rounded end, giving a type of vortical morphology. Such a space-time volume or morphology can be obtained by rotating this space-time region or “area” around the x coordinate in a coordinate system. By using the calculus of integration*, the space-time volume or morphology is shown to be 4Π²Q^-1 space-time to the fifth power. The squared space-time structure taken to the fifth power could be a structure or morphology composed of 10 fused dimensions.

Most physicists conjecture that the universe has 10 dimensions. In this expression, Π² or 10 appears to represent or be the common dimension through all 10 dimensions in the universe on all scales, as the author conjectured earlier. This would appear to be a common dimension also defining spatial-temporal regeneration. Most important, 4Π²Q^-1 is identical to the expression, which the author made explicit, that is implicitly included in Einstein's field equations, and which appears to represent a regeneration parameter of such fields, as noted above.

As 4 Π²Q^-1 space-time to the fifth power appears to represent the same geometry of the universe on various scales, the same expression in Einstein's field equations would also appear to represent the same geometry of regenerative form on all scales. Space-time to the fifth power may also reflect a regenerating universe of vortical morphology through or in 10 dimensions involving Π² .

^{_____________________________________________________________________________________}

*This method of calculating volumes through the rotation of areas is described in all calculus textbooks.

Equation for the logarithmic golden spiral, whose growth factor is Q per 90 degrees of turning relative to the coordinates and origin: r(ϴ) = e^θlnΦ/Π/2 where the end of r defines the growing curve or vector-radius of the spiral; θ is the growing angle with respect to the x axis through which the vector r rotates as it grows and defines the spiral  with the end of its increasing length (within a polar coordinate system), and Φ is the traditional term for the golden ratio. (See Posamentier & Lehmann, 2012). The constant exponents  of e determine the respective distances between the growing spiral's curves, and thereby, its growth-rate, Q, with respect to the origin. Within a complex number, polar-plane-system (or one with more dimensions), this equation could also be r(ϴ) = e^iθlnΦ/Π/2 where i also represents the constant rate of increasing spiral growth or generation over every 90^o irrespective of scale as the vector rotates through 90 degrees with respect to the x axis and y axis and origin, and other co-ordinates. The term Π/2 could also represent such constant-rate-generation of the extending curvature over every 90 degrees with respect to the coordinates and origin. Π/2  is approximately equal to Q.

The generalized equation  representing the family of logarithmic spirals, each of which could have a different, constant growth factor as it turns with respect to its origin, can also simply be r = e^iϴ (Clifford, 1899).  These respectively constant growth factors could represent other transfinite constants of other types of spirals or vortical, generative designs in nature on various scales. Such constants could compose new dimensional constants yet to be discovered.

As represented by or implicit in this generalized equation of the spiral, r is the vector-radius of the growing spiral that increases by some constant factor over each 90 degrees of its rotation (which in the case of the golden spiral would be Q) with respect to the coordinates and origin, and by a rate of 1.718 per 90 degree rotation with respect to each small segment of the growing curve, where i represents an operation of a 90 degree twist or curving turn as described by Clifford. However, when the vector's length remains constant during rotation, the equation defines a circle in a complex number plane. These coordinate systems, implicit and explicit, would appear to be suitable for illustrating and demonstrating the generation of various vortical designs in nature with constant features through space-time. Some of these yet to be discovered. The  numeral 2 appearing in the  equation for the golden spiral, and in some of the equations or expressions of the universal dimensional constants, might denote the duality inherent in the projective imprinting by a template upon the plenum, which generates non-uniformity within reality or space-time, a projected non-uniformity through which the further imprinting generation of vortical designs can be. Might the very exponents composed of 2 in the equations also denote the enhanced contribution of this dynamic property.

                                                                                         Figure1   

 A group of adjacent, vortically shaped succulents. Might such a living group reflect as a generative structure the true, vortically dynamic, yet discontinous morphology of space-time emerging on all scales from a pervasive plenum. The elongated, reddish  structures could be symbolic of the projections of an underlying template within the plenum.

                                                                              Figure 2

Begonia flower displaying a fluid-like, vortical morphology.  This morphology might reflect an inherent generative, dynamic pattern projected within all scales of reality and enabled through the biological dimensionless constant Q or some other dimensionless biological constant.

                                                         Figure 3

 Vortical morphology of a Gastropod shell. Might such a morphology also recapitulate the inherent, dynamically-patterned extension into space-time, through and from a fluid-like plenum, of a universal template manifested through all scales of reality via the constants.

                                                        Figure 4

 A Rose with a fluid-like, vortical morphology, possibly reflecting and recapitulating an inherent, enabled, vortically dynamic structure within the field-fabric of space-time on various scales.

                                                                               Figure 5

A Ranuculus flower with a vortical morphology that may reflect or recapulate a deeper, dynamic pattern or form projected throughout all scales of existence by means of the universal dimensionless constants, some others to be discovered.

                                                                     Figure  6

A group of an integer number of vortical roses. Would this group represent the emergence of vortical morphogenesis with quantum discontinuities from a deeper substratum of existence.

                                                                            Figure 7

Does the vortical morphology of a rose recapitulate the pattern of generative, universal processes?

                                                             Figure 8                                         

A rose with a vortical design. Does the dynamical morphology at the subatomic/quantum level of existence recapitulate the vortical development of a rose?

                                                                     Figure 9

The vortical, maximally adaptive dynamic at the highest of scales could be manifested by this galaxy. This logarithmic, spiral dynamic structure of space-time could, through the regenerative Q constant, recapitulate itself self-similarly through smaller and smaller scales, including those of the biological, to beyond the quantum. This spiral, vortical pattern or formation via Q could recapitulate a dynamic, maximum accommodation or adaptation to all the constraints of those scales through and of space-time. Other morphologies at the cosmological scale, patterned through other regenerative constants, may not be as adaptive or as stable.

This photograph is a copy of one located in the Hubble Heritage Gallery of Images:

http://heritage.stsci.edu/gallery/gallery.html    This website is on the Wikamedia Commons, which allows free use of images.

                                                                Figure 10

A developing rose or a vortical galaxy through space-time? Through all the scales of space-time, the stabilizing, dynamic pattern would be the same.

This image is also from the Hubble Heritage Gallery of Images.

                                                                 Figure S

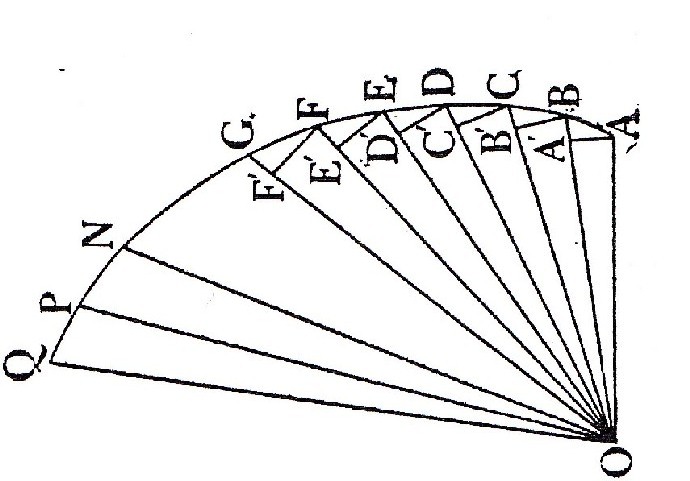
                  A section of the equiangular or logarithmic spiral. From Clifford, 1899.

The angles of 60 degrees and 30 degrees originate at the vertices in all the small, right triangles along the concave of the curve. These small triangles occur through the intersection of the growing spiral radii with the extremely small cords of the arcs of the curve, as described by Clifford. These cords become the extremely small hypotheses of the right triangles, which the radii intersect, creating respectively the tangents and cotangents of the 60 degree and 30 degree angles. These respective constant angles generated on the concave side of the curve make up all equiangular logarithmic spirals. Through the generation of these small, identical triangles, on the concave side of the curve, based on the increasing radii during rotations of 90 degrees of such, the growing spiral is defined. The respective tangent and cotangent of a 60 degree angle and of a 30 degree angle are the same, namely 1.718. The identical tangents and cotangents of these series of 60 degree and 30 degree angles along the concave side of the curve correspond to the constant logarithmic rate of differential growth of the spiral curve. The constant logarithmic rate occurs via the rotation or twist of the growing, end segment of each radius-vector through 90 degrees, forming the 90 degree angle of each identical triangle. This constant growth rate ensues in the generation of the constant, 2.718, also known as the exponential constant, e, which is also a parameter of logarithmic spiral growth. This geometrical analysis of the logarithmic spiral makes manifest the constant parameters or dimensionless constants involved in the generation of the spiral, other than Q at turns, and thereby, become  explicit in or defined in phenomena. Tangent intersections of spiral radii  with the convex side of the spiral curve also produce constant angles. However, each of those angles, and thereby their cotangents, differs respectively with each different logarithmic spiral, that is, is unique for the given logarithmic spiral (Sharp, 2002). For example, for a golden logarithmic spiral, the constant angle due to an intersecting tangent with  the convex side of the spiral is 73 degrees. This angle is indicative of or reflects those logarithmic spirals that grow at the rate of Q. The difference between the types of constant angles respectively generated along the concave and convex sides of the spiral, which takes into account Clifford's analysis, was noted by the author, Michael Lieber. This is a very important, clarifying distinction, which apparently was not seen before.

The dynamical geometrical structure or design represented by Figure S could actually exist as is in the plenum or in a deeper reality within such. This would include the larger triangles generated through the rotating radius or vector, creating radii of increasing magnitude. Our minds, it is proposed, can abstract this design from its plenum seat so that it can be analyzed as a reflection, via our minds, of a projected feature into space-time. This has allowed us to detect additional dimensionless constants and their significance and operation with respect to better understanding existence as it is manifested into space-time. That design, manifested through such constants, might be construed as a platonic form underlying space-time.

As demonstrated in calculus textbooks, the derivative of an exponential function, such as a spiral exponential function, is always equal to the function itself, irrespective of the number of times one undertakes the differentiation process. This means that e, or 1 + 1.718, is a constant component of such a series of identical, or self-similar, derivative/functions, which would apply to the generations of self-similar vortices through different scales of phenomena, physical and biological.

                                                                      References

Clifford, W. 1899, re-published 1946 & 1955. The Common Sense of the Exact Sciences. Dover Publications, New York

Cook, T. A. 1914 (Republished in 1979). The Curves of Life. Dover Publications, Inc. New York.

Einstein, E.  and Infeld, L. 1938. The Evolution of Physics. Simon and Schuster, New York.

Hemenway, P. 2005. Divine Proportion, Phi, In Art, Nature, and Science. Sterling Publishing, Co., New York, NY.

Lieber, M. 1998a. The Living Spiral. A Dimensionless Constant Gives a New Perspective to Physics. Rivista di Biologa/Biology Forum 91: 91-118.  (View PDF of Article.)

Lieber, M. 1998b. Enviromentally Responsive Mutator Systems: Towards a Unifying Perspective. Rivista di Biologia/Biology Forum 91: 425-458.

Lieber, P. 1968. Constants of Nature: Biological Theory and Natural Law. In Towards a Theoretical Biology I, C.H. Waddington (ed), University of Edinburgh Press, Edinburgh, pp. 180-204.

Lieber, P. 1969. Aspects of Evolution and a Principle of Maximum Uniformity In Towards a Theoretical Biology II, C.H. Waddington (ed), University of Edinburgh Press, Edinburgh, pp. 219-316.

Lieber, P. 1969(b).  Categories of  Information. In Contribution to Mechanics, edited by D. Abir. Pergamon Press, Oxford, pp. 87-106.

Livio, M. 2002. The Golden Ratio. The Story of Phi. The World's Most Astonishing Number. Broadway Books, New York.

Peat, F. D. 1996. Infinite Potential. The Life and times of David Bohm. Helix Books, Addison-Wesley, Reading, Massachusetts

Penrose, R. 1994. Shadows of the Mind. A Search for the Missing Science of Consciousness. Oxford University Press.

Pickover, C. 1990. Computers Patterns Chaos and Beauty. St. Martin's Press, New York

Posamentier, A. & Lehmann, I., 2012. The Glorious Golden Ratio. Prometheus Books, Amherst, NY

Sharp, J. 2002. Spirals and the Golden Section. Nexus  Network Journal. Vol. 4, No. 1: 59-82.

                                                                              Postscript:

  The Unity of Phenomena on Different Scales as Exemplified by the Research of Albert Einstein and Paul Dirac: The Relevance of  a New Universal Constant.

This is a publication in the journal, Cosmos and History:  The Journal of Natural and Social Philosophy, vol.18, no. 1, 2022. Pages 572-576.  See also references in Bibliography section.

                               Part of which was originally presented here in March, 2015, and recently removed.

Statement by Michael Lieber, fall 1981: Through the universals, the mind has been defined by God. This connection to the infinite gives the human being the capacity for infinite development. In this period of growing pessimism, where the human being is seen as a liability to its own existence, this view of the human mind should provide tremendous hope and optimism for the beneficial evolution of the human race and its biosphere.

                                      SOME CONSIDERATIONS RELATING TO THEORETICAL BIOLOGY*

                                                                                by

                                                                    Professor Paul Lieber

                                               University of California, Berkeley, April, 1961  

Since 1943, I have been engaged in a study relating to the universal-physical constants leading to a number of inferences and conjectures, which may be relevant to furthering our capability in comprehending the life process. Concurrently, I was also engaged in studies on the foundations of classical mechanics and hydrodynamics in which the thinking was naturally influenced by the work done on the universal-physical constants, and conversely. The cross-fertilization and interplay of ideas springing forth from what may appear as completely separated areas of investigation has been constructive in producing a somewhat coherent picture relating these apparently disjointed studies.

I have been especially concerned with the task of resolving a fundamental conceptual dilemma arising in Hertz's mechanics, and which refers specifically to the problem of materializing in a precise way the geometrical connections invoked by Hertz, and upon which, his theory rests in a crucial manner. An attribute of matter has been isolated, namely impermeability, which achieves this end conceptually at least, and which appears to have an equal significance in resolving a fundamental question arising in the study of the universal-physical constants. This correspondence in turn renders a concept which may appear significant toward evolving a way of thinking constructively and systematically about biological phenomena.

My work in classical mechanics suggests with increasing force and conviction the operation in nature of a universal correspondence principle, which may be regarded as an extension of the correspondence principle formulated by Niels Bohr; and which may find its fullest and most perfect expression in the biological process. According to the extended correspondence principle, appropriately extended laws of classical mechanics would, for example, bear direct and complete rather than asymptotic correspondence to the principles of relativistic mechanics as they do in the sense of Bohr. This conjecture implies, of course, that the present statements of the principles of classical mechanics are in a sense incomplete and that a more complete, non-relativistic expression of them operates within the domain of classical mechanics; and that this form is in a certain sense incomplete rather than in asymptotic correspondence with the principles of relativistic and quantum mechanics.

In this connection, it may be hard to imagine a sense in which the known principles of classical mechanics may be regarded as being incomplete. It is now conventional to regard them as deterministic, and it is accordingly tacitly assumed that in principle they render coordinate information with arbitrary accuracy. That is, that in principle there exists no upper bound upon the accuracy of coordinate information sought and obtainable in numerical representation. This, however, is but a conjecture which does not have its basis in proof. The number of solutions obtained by analytical representation for the coordinates of mechanical systems is indeed strikingly limited by their complexity; as reflected, for example, by the unsolved classical problem of three bodies. The fact that the fundamental connections between classical mechanics and thermodynamics remain to be grasped suggests a possible incompleteness in the principles of classical mechanics as they are known.

There is indeed now reason to believe that such an extended form of the principles of mechanics may find expression as a variational principle in which space and time are interconnected in a way which corresponds to their metric connection in relativity. It now appears that this variational principle may be obtained by appropriately extending the differential variational principles of Gauss and Hertz to an integral form. In so doing, it would express a condition of maximum uniformity in terms of an integral space-time measure. There is strong reason to conjecture that this variational principle would render accessible information relating to the behavior of many-body systems, which has hitherto remained inaccessible in terms of known principles of classical mechanics. The three-body problem may be considered as a case in point. This conjecture has grown out of a theorem, based on the mechanics of Gauss and Hertz, which asserts that the collective motion of a many-body system is subject to a law concerning the distribution of a scalar measure of all the internal forces prevailing within the system. This law may provide a bridge for linking at least conceptually and possibly analytically the mechanics and thermodynamics of many-body systems. In so doing, it is quite conceivable that fundamental information about cooperative phenomena, which are so characteristic in organisms, will evolve. It is believed that the extended variational principle referred to above will provide such a bridge.

The theorem relating to the distribution of internal forces in a many-body system has also rendered information basic to the conception and formulation of what appears to be a fundamental variational principle for the hydrodynamics of viscous fluids. This variational principle seems among other things to resolve two long outstanding paradoxes of hydrodynamics, and implies a direction connection between asymmetric and time-dependent motions. What is equally interesting is that according to this variational principle, vortex and spiral motions are indeed preferred in non-uniform flows. Although this variational principle has been established as a theorem on the basis of the principle of conservation of matter, it renders much more information about flows than has been inferred from this conservation law directly. Its formulation may indeed be regarded as a synthetic technique for extracting the information cited above. Noting this variational principle is relevant here since it conditions cooperative phenomena in fluids and furnishes an example of how fundamental and new information about flows is obtained by such a formulation. This principle asserts that a measure of uniformity is a maximum for real flows. It is accordingly related in some sense to the extended variational principle mentioned above pertaining to many-body systems.

A biological system may be regarded as a complex consisting of component systems, which, according to our conventional way of thinking, are individually either predominately classical or non-classical in their operation. For example, the hydrodynamics of such a complex may be assumed to be governed by the laws of classical mechanics and thermodynamics, whereas the molecular chemistry is essentially quantum mechanical and quantum electrodynamical in nature. It is the strong and highly controlled interplay between these component systems which is indeed overwhelmingly characteristic of biological material. It is difficult to conceive how this interplay and control can find its expression in a correspondence principle which emphasizes their connections as being asymptotic rather than universal. Conversely, this observation concerning the function of biological material evokes compulsively the operation of a universal correspondence principle which emphasizes the strong rather than the asymptotic connections between the principles governing the function of their components.

My research work pertaining to a study of the structure of the universal-physical constants led to some interesting and unusual conclusions. These require careful re-examination and possibly both amplification and extension before they can be submitted as results for publication. One conclusion reached under this study, which may have fundamental implications to biology, is that the universal-physical constants imply the existence of a class of physical phenomena whose manifestations are detectable but nevertheless in principle are not amenable to control. In this sense, this class of phenomena are in principle inaccessible to direct observation and manipulation by the application of impressed forces. The implication to biology suggested here refers more specifically to the operation of biological control systems, in which the control mechanisms are in a sense inaccessible to disturbances emanating from the systems which they control and dominate. The universal physical-constants thus appear to provide connections between a class of non-observable and observable physical phenomena, and these connections may prove fundamental in the function and control of biological processes. Another related conjecture obtained from the study of the universal constants is that they are manifestations of elementary space-time structures rather than of elementary particles.

The search for elementary particles in physics appears motivated by and may be attributed to a conceptual framework which implicitly adheres to the idea that all matter is composed of elementary bodies and that any and all of the changes occurring therein may be attributed to displacements in space and time of those elementary particles. The identification with the universal-physical constants of invariant space-time structures, which propagate as a helix by regeneration rather than by bodily displacement, calls for a re-examination of the validity and appropriateness of the conceptual framework in which the notion of an elementary particle is implicitly cast. The notion of an elementary body and its displacement implies that it is imbedded in a space which can accommodate its displacement, in such a way, that it is always composed of the same material. The primitive idea of localizing a body by affixing to it a label carries this implication, since if the material changes then the label is destroyed. The identification of universal space-time structures rather than elementary particles with the universal constants, and their inaccessibility to observation, leads to the conjecture that they are imbedded in an impermeable, material continuum and propagate by regeneration rather than by bodily displacement. These finite structures embody both corpuscular and wavelike properties. Their corpuscular properties, however, differ fundamentally from those of an elementary particle in that the material constituting an elementary structure is continuously changing consistent with the requirements that the structure remain invariant. The idea of localizability and thus labeling can, however, be retained under these conditions, as well, if the labels are identified with material points rather with material bodies. In this case, however, the elementary particles are the material points of a material continuum, in terms of which, the concept of localizability finds its purest and most precise expression.

Biological control systems are striking in their precision of operation and power of organizing the function of macro-systems within an organism. What is an equally striking fact, and which must also be accommodated by any acceptable way of thinking about biological systems, is that these control systems are materialized in but a small fraction of the material constituting the organisms, which they control. These observations compulsively suggest that the material of which the control systems are made may be inaccessible to observation and thus to direct experiment. They may accordingly be identified with the class of physical phenomena, which according to the universal-physical constants, are in principle inaccessible to direct experiment. This inaccessibility would account for the immunity enjoyed by the biological control systems with respect to the functions of the macro-systems, which they control and dominate. The universal-physical constants imply a connection, as noted above, between a class of non-observable and observable phenomena, which are engaged irreversibly so to insure the invariance of elementary spatial temporal structures in the non-observable domain. It is here conjectured that these structures may be fundamental to biological control systems, and their invariance and inaccessibility may account for the immunity which they appear to enjoy with respect to observable changes.

*First published on this website. Copyright (c) by Michael Lieber                          Home

Paul Lieber also wrote in December 14, 1988:

[Paul Lieber met with A. Einstein circa 1952 to discuss the Dimensional Universal Physical Constants and most likely this deep issue of their designation. Einstein’s comments or thinking in this regard were never written or transcribed, nor presented by Paul Lieber, as far as I know.]

                                                     The following person was a friend to and a collaborator with both Paul Lieber and the author.

                                                                               Copy  of a Letter  to Professor Jan Kryspen, M. D.

                                                                                      July 12, 1999

Mind seizes that which is constant in nature or seizes the generative basis of such constancy. This is perhaps through the generation of its own constant features. The unity within the object/subject "dichotomy" is constancy or its generative basis. Hence, force defines that unity. What appears to us as being the absolute object/subject dichotomy may only be the dynamic pattern of this constant unity or constancy.

                                                                                                        July, 2024